functor
Functor 类型类只需要一个定义: fmap

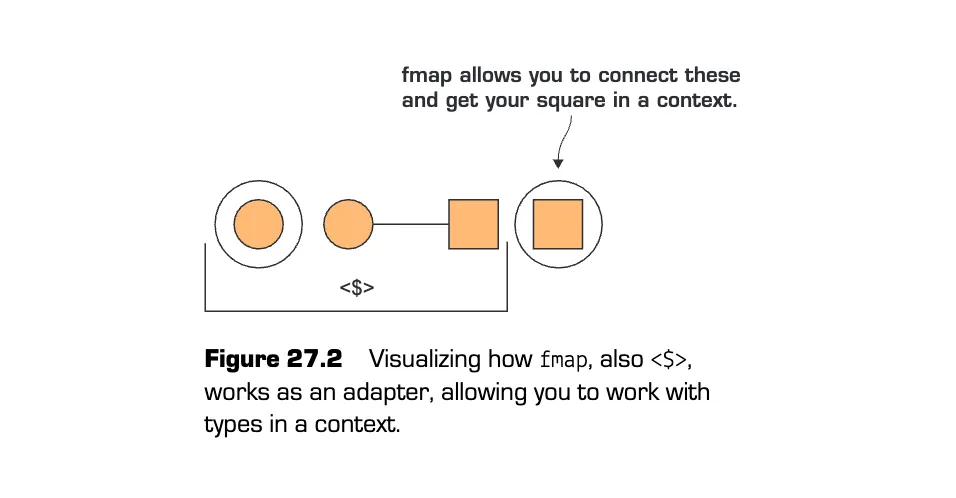
fmap 提供了一个适配器,如图 所示。请注意,我们使用的是 <$>,它是 fmap 的同义词(除了它是二元运算符而不是函数)。
学习 Functor 是理解函数式编程中的一个重要概念,尤其是在像 Haskell 这样的语言中。Functor 提供了一种抽象的方式来操作包含在上下文中的数据。它可以类比为一种容器或包装器,允许你对容器内的数据应用函数,而不必关心数据的具体结构。
Functor 的定义
Functor 是一个类型类,定义了一个 fmap 函数,它接受一个函数并将其应用到 Functor 内部的值上。
在 Haskell 中,Functor 的类型类定义如下:
class Functor f where
fmap :: (a -> b) -> f a -> f bf是一个容器或上下文,它包裹了一些值。比如列表、Maybe、Either都可以看作是Functor。fmap接受一个函数(a -> b),以及一个Functor(f a)并将该函数应用到Functor内部的值,从而返回另一个Functor(f b)。
直观理解
可以把 Functor 想象成一种包装器。fmap 是一种工具,它帮助你打开包装,对里面的内容应用函数,然后再重新封装起来。
例如,在列表 [] 上,fmap 就是把函数应用到列表的每一个元素上:
fmap (*2) [1, 2, 3]
-- 结果是 [2, 4, 6]
在 Maybe 上,fmap 允许你对一个可能包含值的结构进行操作:
fmap (*2) (Just 5)
-- 结果是 Just 10
fmap (*2) Nothing
-- 结果是 Nothing
Functor 的意义
Functor 抽象的核心思想是 在不改变结构的情况下操作其中的值。具体来说,fmap 会保留容器(或上下文)的结构,而只改变其中的内容。
具体例子
-
列表
[]列表是一个最简单的
Functor,fmap就是把函数作用到列表的每个元素:fmap (+1) [1, 2, 3] -- [2, 3, 4] -
Maybe
Maybe是一个包含Just或Nothing的类型,fmap会对Just中的值应用函数,而Nothing则保持不变:fmap (*2) (Just 5) -- Just 10 fmap (*2) Nothing -- Nothing -
Either
Either类型可以用来表示错误或成功的结果。Either的Functor实现只对Right中的值应用函数,Left中的值表示错误,保持不变:fmap (+1) (Right 10) -- Right 11 fmap (+1) (Left "Error") -- Left "Error"
Functor 定律
为了使 fmap 在不同类型中行为一致,Functor 必须遵循两个定律:
-
同一性定律(Identity Law)
对任意的
x,fmap id x == x。即应用id(恒等函数)不会改变Functor的内容。fmap id [1, 2, 3] == [1, 2, 3] -
组合性定律(Composition Law)
对任意函数
f和g,fmap (f . g) == fmap f . fmap g。即将组合后的函数应用在Functor上,等价于先分别应用每个函数再组合结果。fmap ((+1) . (*2)) [1, 2, 3] == fmap (+1) (fmap (*2) [1, 2, 3]) -- 结果都为 [3, 5, 7]
为什么 Functor 很重要?
- 抽象化处理:通过
Functor,你可以对不同的数据结构(列表、Maybe、Either等)应用相同的操作,而无需关心它们的具体实现细节。 - 提升代码的可组合性:
fmap提供了一种标准化的方式将函数作用于各种容器中的值,这让代码更加简洁和可组合。 - Functor 是更高层次抽象的基础:
Functor是Applicative和Monad等更复杂抽象的基础,因此理解Functor是掌握 Haskell 高阶特性的第一步。
总结
Functor是一个抽象概念,用于描述如何对包含值的上下文(如列表、Maybe等)应用函数。fmap是核心操作,它允许你对 Functor 内部的值进行操作,而不改变外部的结构。Functor遵循两个定律:同一性定律和组合性定律,确保操作的一致性。
通过学习 Functor,你可以在 Haskell 中更自然地理解和使用函数式编程中的抽象和组合理念。
Functor 类型类允许您将普通函数应用于容器(例如 List )或上下文(例如 IO 或 Maybe )内的值。如果您有一个函数 Int -> Double 和一个值 Maybe Int ,则可以使用 Functor 的 fmap (或 <$> 运算符)将 Int -> Double 函数应用于 Maybe Int 值,从而产生 Maybe Double 值。函子非常有用,因为它们允许您将单个函数与属于函子类型类的任何类型重用。 [Int]、 Maybe Int 和 IO Int 都可以使用相同的核心函数。